Circle Exercise for Secondary Students

 

This article is about Circle and the worksheet and its' properties.

Definition of Circle

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the center; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the center is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. A circle is a line drawn at a fixed distance from a point. The point is called the center, and the line that is drawn a fixed distance from it is called the circumference. The distance from the center to the circumference is the radius. A line joining one part of the circumference to another part of the circumference is known as a chord. A chord that goes through the center of a circle is diameter and has twice the length of the radius.

Isosceles Triangle

Look at the picture below about an isosceles triangle from a circle.  Two Radii and a chord make an isosceles triangle.

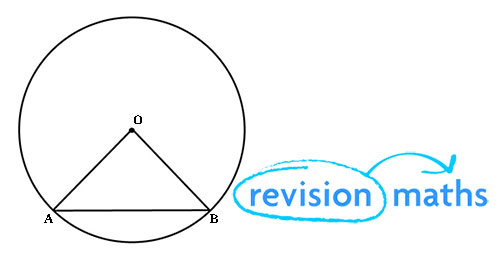
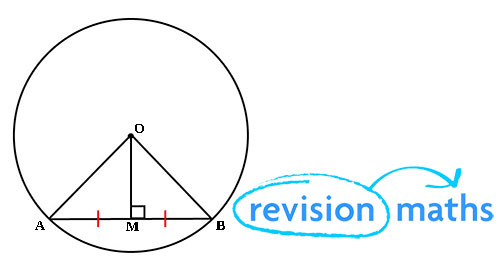
Perpendicular Chord Bisection

From the picture above, we can make the perpendicular from the center. The perpendicular from the centre of a circle to a chord will always bisect the chord (split it into two equal lengths).

 

Angles Subtended on the Same Arc

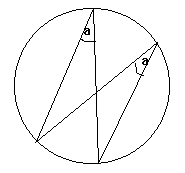
Angles formed from two points on the circumference are equal to other angles, in the same arc, formed from those two points.

Angle in a Semi-Circle

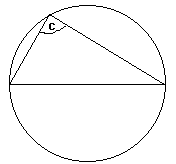
Angles formed by drawing lines from the ends of the diameter of a circle to its circumference form a right angle. So c is a right angle.

Proof

We can split the triangle in two by drawing a line from the centre of the circle to the point on the circumference our triangle touches.

We know that each of the lines which is a radius of the circle (the green lines) are the same length. Therefore each of the two triangles is isosceles and has a pair of equal angles.

But all of these angles together must add up to 180°, since they are the angles of the original big triangle.

Therefore x + y + x + y = 180, in other words 2(x + y) = 180.
and so x + y = 90. But x + y is the size of the angle we wanted to find.

Tangents

A tangent to a circle is a straight line that touches the circle at only one point (so it does not cross the circle- it just touches it).

A tangent to a circle forms a right angle with the circle's radius, at the point of contact of the tangent.

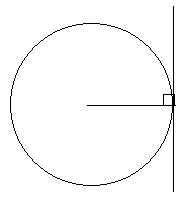
Also, if two tangents are drawn on a circle and they cross, the lengths of the two tangents (from the point where they touch the circle to the point where they cross) will be the same.

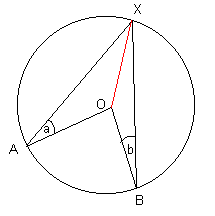
Angle at the Centre

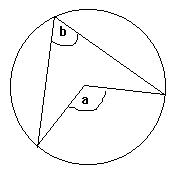
The angle formed at the centre of the circle by lines originating from two points on the circle's circumference is double the angle formed on the circumference of the circle by lines originating from the same points. i.e. a = 2b.

Proof

You might have to be able to prove this fact:

OA = OX since both of these are equal to the radius of the circle. The triangle AOX is therefore isosceles and so ∠OXA = a
Similarly, ∠OXB = b

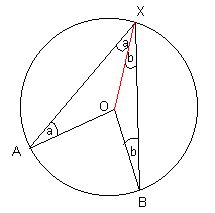
Since the angles in a triangle add up to 180, we know that ∠XOA = 180 - 2a
Similarly, ∠BOX = 180 - 2b
Since the angles around a point add up to 360, we have that ∠AOB = 360 - ∠XOA - ∠BOX
= 360 - (180 - 2a) - (180 - 2b)
= 2a + 2b = 2(a + b) = 2 ∠AXB

Alternate Segment Theorem

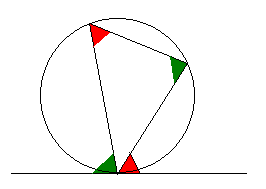
This diagram shows the alternate segment theorem. In short, the red angles are equal to each other and the green angles are equal to each other.

Proof

You may have to be able to prove the alternate segment theorem:

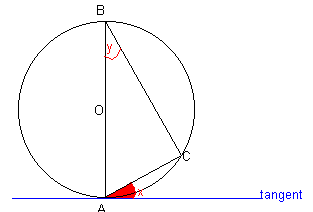
We use facts about related angles

A tangent makes an angle of 90 degrees with the radius of a circle, so we know that ∠OAC + x = 90.
The angle in a semi-circle is 90, so ∠BCA = 90.
The angles in a triangle add up to 180, so ∠BCA + ∠OAC + y = 180
Therefore 90 + ∠OAC + y = 180 and so ∠OAC + y = 90
But OAC + x = 90, so ∠OAC + x = ∠OAC + y
Hence x = y

Cyclic Quadrilaterals

A cyclic quadrilateral is a four-sided figure in a circle, with each vertex (corner) of the quadrilateral touching the circumference of the circle. The opposite angles of such a quadrilateral add up to 180 degrees.

Area of Sector and Arc Length

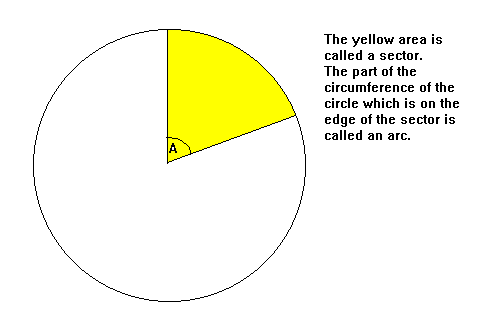
If the radius of the circle is r, Area of sector = πr2 × A/360 Arc length = 2πr × A/360

In other words, area of sector = area of circle × A/360. arc length = circumference of circle × A/360

Exercise for Circle 

 Learning Objectives:

1. To Understand the General and Standard Form of a circle

2. Change General to Standard form of a circle

 Example: 

Change this following general form of circle into its standard form!

x² + y² − 2x − 4y − 4 = 0

Solution:

x² + y² − 2x − 4y − 4 = 0

·         First step: collect all x and y together. : (x² − 2x) + (y² − 4y) − 4 = 0

·         Second step: Put constant on right side. : (x² − 2x) + (y² − 4y) = 4

·         Third Step: Complete the square for x (take half of the −2, square it, and add to left and right sides).

(x² − 2x + (−1)²) + (y² − 4y) = 4 + (−1)²

·         Fourth step: Repeat the third step for y (take half of the −4, square it, and add to left and right sides).

(x² − 2x + (−1)²) + (y² − 4y + (−2)²) = 4 + (−1)² + (−2)²

·         Fifth Step: Simplify the result.

(x² − 2x + 1) + (y² − 4y + 4) = 9

 The standard form will be like:

(x − 1)² + (y − 2)² = 3².

Well done.

		See also :  Properties of Circle and its example Sine and Cosine Rules Visit our Website: Sebuahtutorial.com

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Try It!

Change the following general form into standard form!

x² + y² − 4x + 2y − 4 = 0